Konisk pendel

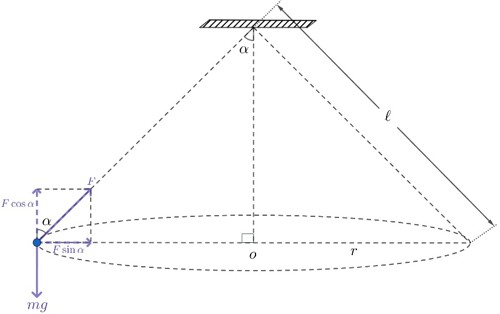
En kula hänger i en tråd som sättes i rotation och bildar en cirkulär rörelse med konstant hastighet. Vinkeln mellan lodlinjen och snöret är \(\alpha\). De krafter som verkar på kulan framgår av figuren nedan. Trådens rotation bildar formen av symmetrisk kon, därav namnet konisk pendel.

Kulan påverkas av två krafter, tyngden \(mg\) och spännkraften \(F\) från tråden. Eftersom banan är en horisontell cirkel, måste kraftresultanten vara horisontell och riktad mot banans centrum. Krafterna i vertikal led balanserar varandra.

Vi får

$$F \cos \alpha = mg ⇒ F = \frac{mg}{\cos \alpha} \hspace{2cm} (1)$$

Tråden längd är \(\ell\), då blir banradien \(r\)

$$r = \ell \sin \alpha \hspace{2cm} (2)$$

Kraftresultaten enligt figuren är: \(F \sin \alpha\)

Centripetalaccelerationen: \(a_c = \frac{4\pi^2 r}{T^2}\)

Kraftekvationen är:

$$F\sin\alpha = ma_c = m\frac{4\pi^2 r}{T^2}$$

insättning av ek (1) och (2) ger

$$\frac{mg \sin\alpha}{\cos\alpha} = m\frac{4\pi^2 \ell \sin\alpha}{T^2} ⇒$$

Det är omloppstiden för en konisk pendel. Som vi ser är omloppstiden oberoende av massan.

• g = gravitationsaccelerationen
• \( \alpha \) = vinkeln bildad mellan center linjen och pendeln
• T = svängningstiden
• \( \ell \) = längden av pendeln