Plan pendel

\[T = 2\pi \sqrt{ \frac{\ell}{g} }\]
\( \ell \) = pendelns längd (\(m\))
g = gravitationsaccelerationen (\(m/s^2\))
Notera att omloppstiden för en matematisk pendel är oberoende av massan.
I figuren ser vi en kula som hänger i ett snöre som svänger fram och tillbaka i ett plan. Jämviktsläget är i lodlinjen (vertikalt). Om kulan är liten i förhållande till snörets längd och snöret lätt har vi en så kallat matematisk pendel.
De krafter som verkar på pendelkulan framgår av figuren. Luftmotståndet är försumbart. Svängningens elongation är cirkelbågen \(s\), och den återförande kraften \(F\) är tyngdkraftens komposant längs bågens tangent.
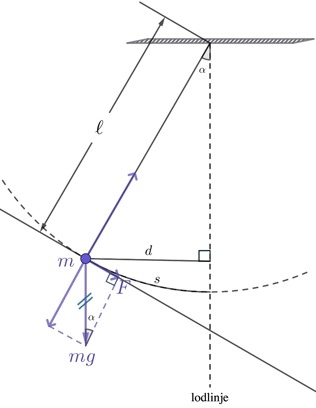
Likformiga trianglar ger
\[\frac{F}{mg}=\frac{d}{\ell}⇒ F = mg\cdot \frac{d}{\ell}\]
När \(\alpha\) är liten kan \(d\) approximeras med \(s\) och vi får
\[F = \frac{mg}{\ell}\cdot s\]
Härmed är den återförande kraften \(F\) proportionell mot elongationen \(s\) och vi får en harmonisk svängning. Proportionalitetskonstanten \(\frac{mg}{\ell}\) motsvarar fjäderkonstanten \(k\) vid en fjädersvängning. Vi får då för svängningstiden med liten utslagsvinkel
\[T = 2\pi \sqrt{ \frac{m}{k} } ⇒ 2\pi \sqrt{ \frac{\ell}{g} }\]
Vid längre utslagsvinkel, t ex 45 grader är pendelrörelsen inte längre harmonisk och svängningstiden blir något förlängd, \(4\%\) längre än den tid man får med sambandet \(2\pi \sqrt{ \frac{\ell}{g} }\)
Som vi ser är omloppstiden oberoende av massan.
- \( \ell \) = pendelns längd (\(m\))
- g = gravitationsaccelerationen (\(m/s^2\))
