Transversatsen & topptriangelsatsen

Transversalsatsen

Transversalsatsen säger att en parallelltransversal som delar två sidor av en triangel, delar dessa båda sidor i samma förhållande, vilket gör att 

\[ \frac{a}{b} = \frac{c}{d} \text{ eller } \frac{b}{a} = \frac{d}{c}  \]

om vi använder beteckningarna för trianglarnas sidor enligt figuren nedan.

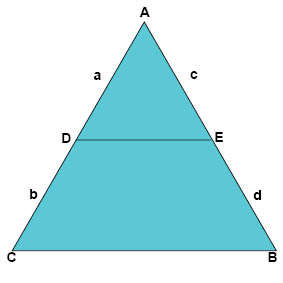
Topptriangelsatsen

Topptriangelsatsen talar om för oss att den topptriangel (ADE i figuren nedan) som bildas av en parallelltransversal är likformig med hela triangeln (ABC i figuren nedan).

vi får följande likheter

\[ \frac{DE}{CB} = \frac{AD}{AC} = \frac{AE}{AB} \]